How a Transformer with Attention Works?
I am not going to talk about how attention works here. Because I am not a youtuber who can explain attention in 30seconds shorts. I strongly feel explaining attention in single blog is near impossible tasks. To understand how the real world attention (Multi head attention) works someone needs to understand simplified attention -> Self attention -> Causal attention -> Multi-head attention. Jumping straight to multi-head attention and talk about it doesn’t make sense. I will write detailed blogs on each type of attention in following days, but in this blog I am going to assume you know how attention works otherwise you assume atttention mechanism is like superman formula which helps LLM to understand long sentences without missing the context.
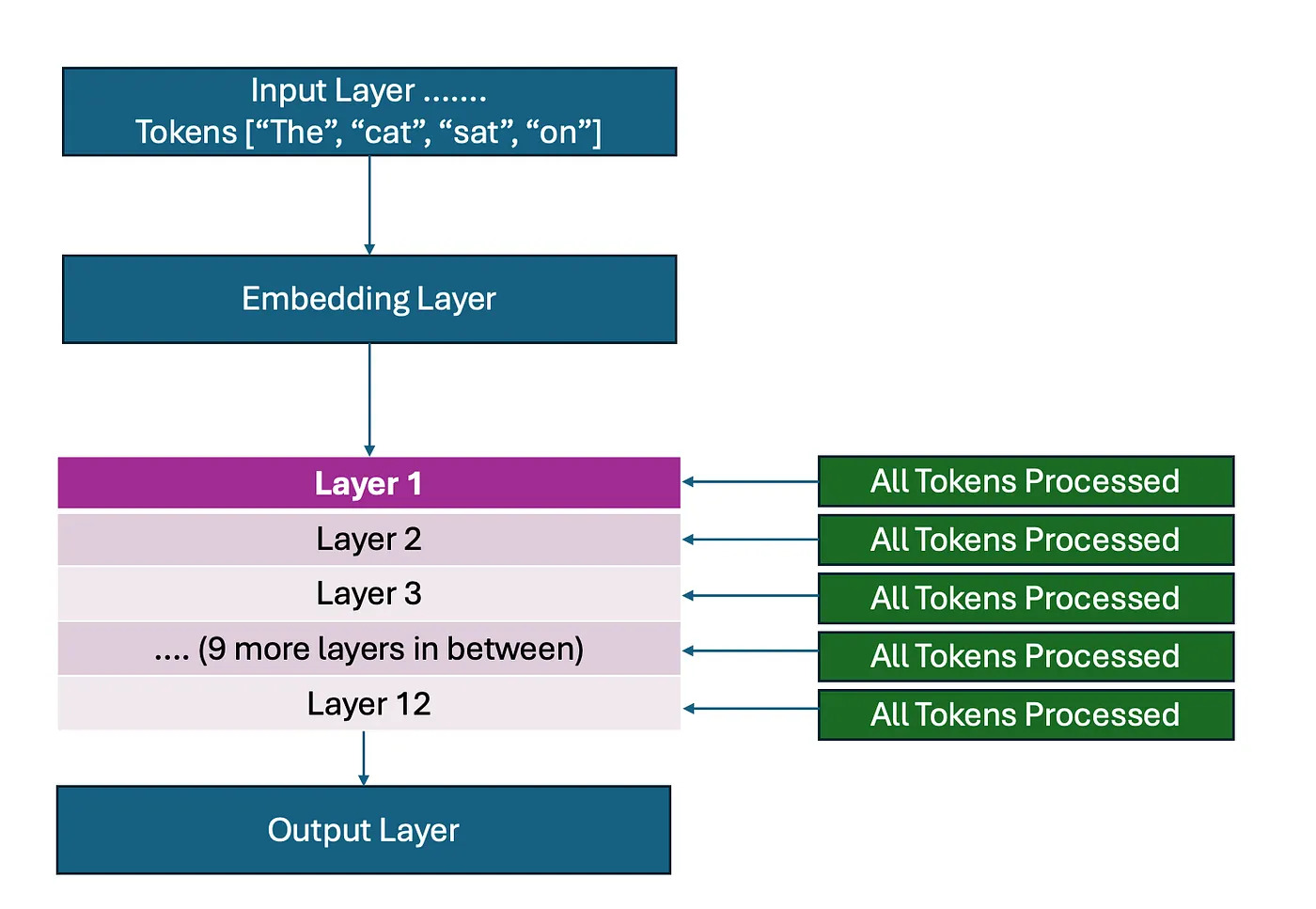
Okay with that, below is how regular transformer works with full attention going on in each layer.
# Every token goes through EVERY layer: Layer 1: - "The" (simple word) → Full attention + 100M parameter processing - "sophisticated" (complex) → Full attention + 100M parameter processing - "algorithm" (complex) → Full attention + 100M parameter processing - "processes" (medium) → Full attention + 100M parameter processing - "data" (simple) → Full attention + 100M parameter processing - "efficiently" (medium) → Full attention + 100M parameter processing Layer 2: REPEAT for all tokens Layer 3: REPEAT for all tokens ... Layer 12: REPEAT for all tokens
KV Cache: The Memory System you must know to understand Attention
In attention, each token creates Key and Value vectors. During text generation, we
don’t want to recompute these for
already-processed tokens!
Without KV Cache
Step 1: Generate "cat" - Compute: K["The"], V["The"] - Generate: "cat" Step 2: Generate "is" - Compute: K["The"], V["The"] ← WASTE! Already computed - Compute: K["cat"], V["cat"] - Generate: "is" Step 3: Generate "sleeping" - Compute: K["The"], V["The"] ← WASTE! - Compute: K["cat"], V["cat"] ← WASTE! - Compute: K["is"], V["is"] - Generate: "sleeping"
With KV Cache:
Step 1: Generate "cat"
- Compute: K["The"], V["The"]
- Cache: Store K["The"], V["The"] in memory
- Generate: "cat"
Step 2: Generate "is"
- Retrieve: K["The"], V["The"] from cache ← FAST!
- Compute: K["cat"], V["cat"] (only new token)
- Cache: Store K["cat"], V["cat"]
- Generate: "is"
Step 3: Generate "sleeping"
- Retrieve: K["The"], V["The"], K["cat"], V["cat"] from cache
- Compute: K["is"], V["is"] (only new token)
- Generate: "sleeping"
# Each layer has its own KV cache
kv_cache = {
'layer_0': {
'keys': [[k_the], [k_cat], [k_is], ...],
'values': [[v_the], [v_cat], [v_is], ...]
},
'layer_1': {
'keys': [[k_the], [k_cat], [k_is], ...],
'values': [[v_the], [v_cat], [v_is], ...]
},
# ... for each layer
}KV Cache Memory Usage Example:
# Let's assume 12 layer transformer with 1000 tokens
layers = 12
sequence_length = 1000
hidden_dimension = 768
# KV Cache memory per layer for Keys and Values
kv_memory_per_layer = sequence_length * hidden_dimension * 2
total_kv_memory = layers * kv_memory_per_layer
print(f"Total KV Cache: {total_kv_memory / 1e6:.1f}M parameters worth of memory")
# Output: Total KV Cache: 18.4M parameters worth of memory ----> Woah it's a lot right?So now we know Attention is best and KV Cache is best. But why do all of the tokens
(simple, medium and complex) need same level of attention? What if I focus more on complex words many times but
simple words only just a glance ? That’s where MOR (Mixture of Recursions) comes, Make way guys……
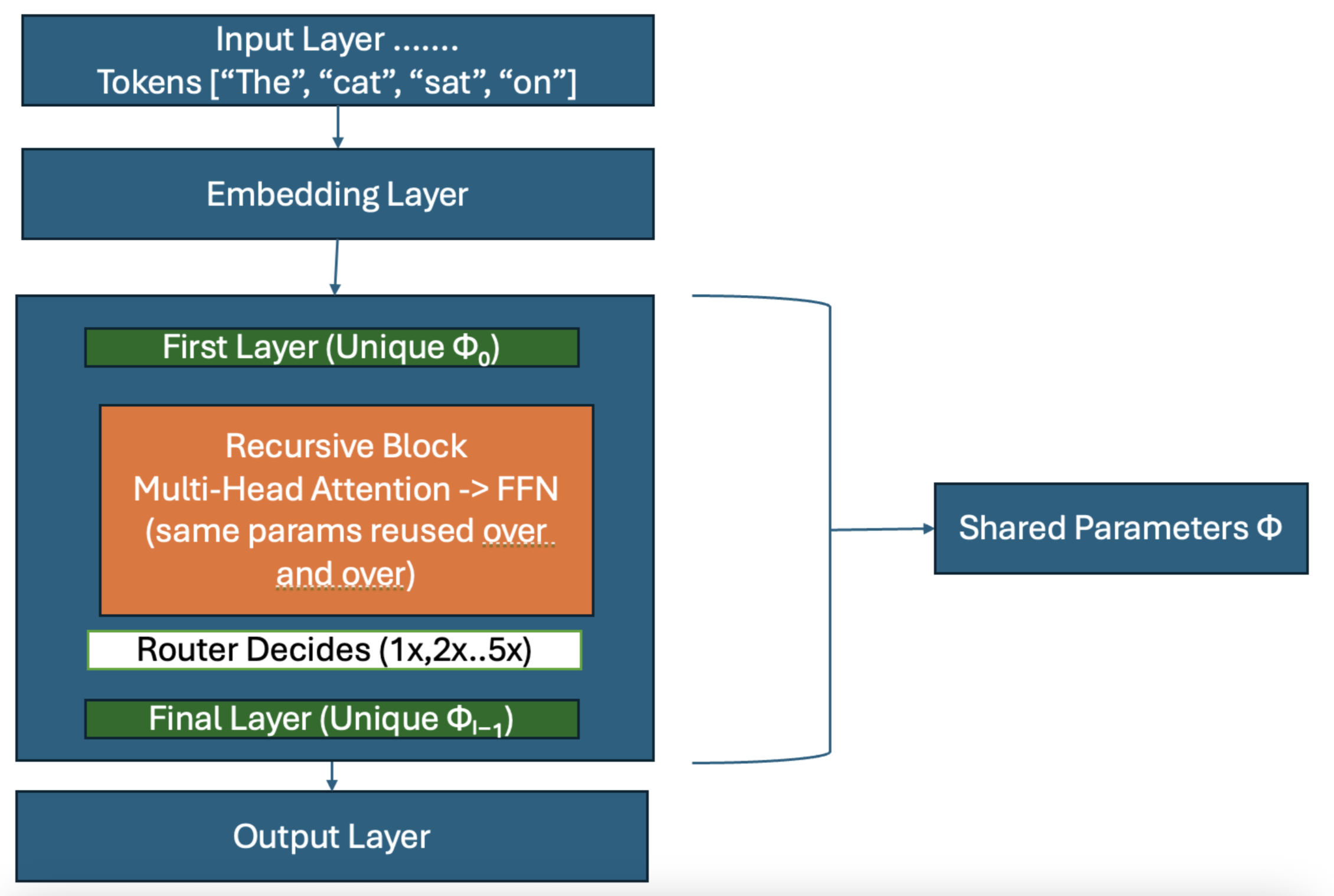
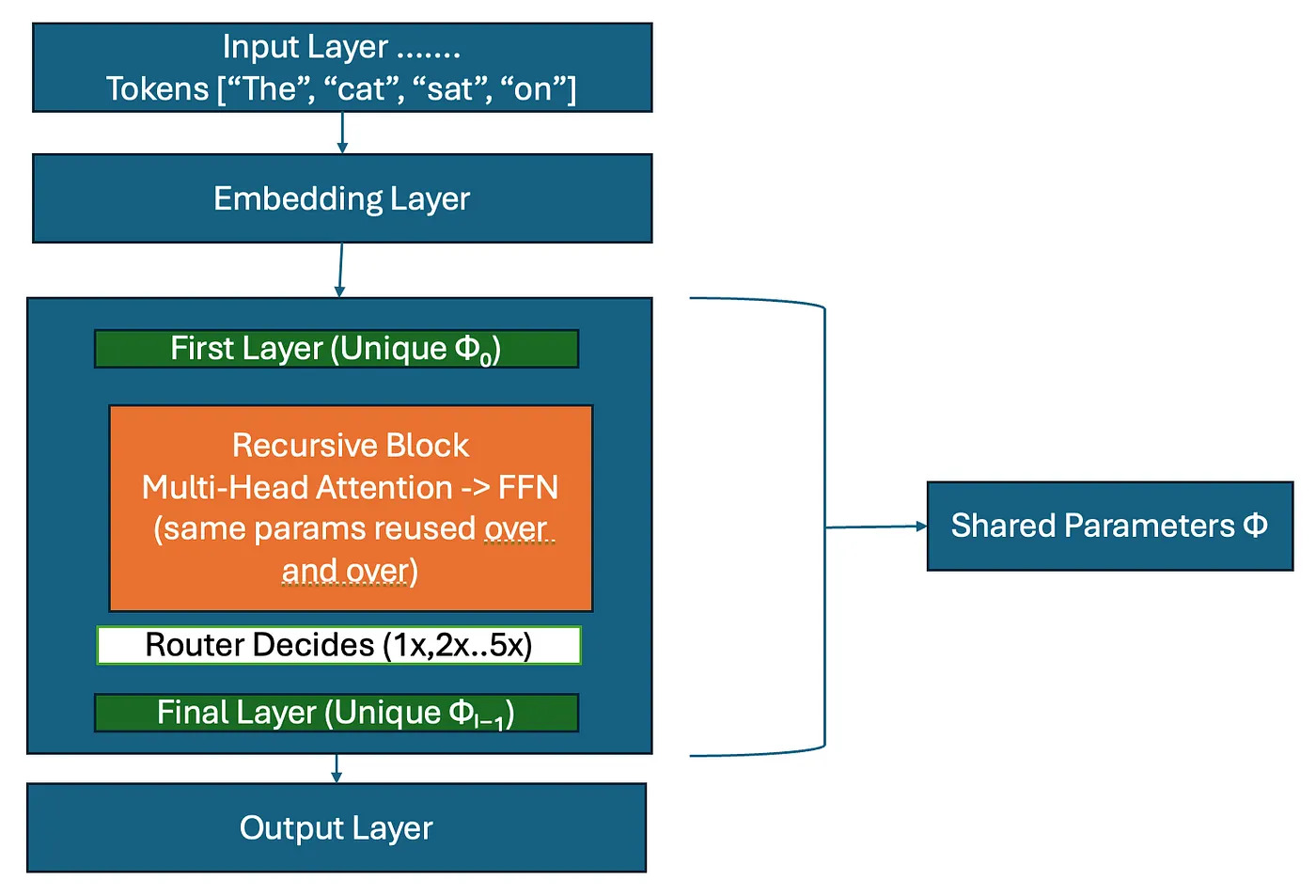
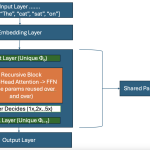
Just keep Input layer, embedding layer and output layer as same. But replace the in
between layers with full attention to recursive block. Just like in real life,
1. Simple concepts need basic processing
2. Complex concepts need deep thinking
3. We shouldn’t waste resources on obvious things
Recursive Block will have First layer -> This will have unique parameters to
understand the first pass of tokens after embedding layer. This is when Router
function decides which is simple token and which is complex token. Note the word router
function we will get back to this shortly. Once router decides simple tokens
iterates only once in recursive block but complex token iterates in recursive block multiple times using same
parameters (no new parameters so no new layers so it saves us ton of compute and memory). This goes into Final layer
with unique parameters and Transformer’s decoder decodes to output layer.
Before I will show you this MOR with real example, let me talk bit about Router Function. There are two
types of router functions,
1. Token Choice Routing — It’s like individual decision making. Like each token
decides itself whether this is simple or complex,
routing_decisions = {
"The": 1, # Simple article
"sophisticated": 3, # Complex adjective
"algorithm": 2, # Technical term
"processes": 2, # Action verb
"data": 1, # Simple noun
"efficiently": 2 # Adverb
}2. Expert Choice Routing — This is like there are limited seats availability. Calculate complexity scores for each token and pick only top k tokens out of it. This is like trade-off. Below is the example,
# From ["The", "sophisticated", "algorithm", "processes", "data", "efficiently"] # Select top 60% → ["sophisticated", "algorithm", "processes"] # we will drop poor kid "efficiently" :( :( :(
Now let’s get back to the track, how MOR works (Remember ? Basically this is recursive block you saw in above architecture)
Step 1: Router Decision
router_decisions = {
"The": 1, # Simple word → 1 recursion
"brilliant": 2, # Descriptive → 2 recursions
"scientist": 3, # Complex role → 3 recursions
"discovered": 2, # Action → 2 recursions
"amazing": 1, # Simple adjective → 1 recursion
"results": 2 # Outcome → 2 recursions
}Step 2: Recursion Block
Recursion 1: All Tokens are passing
Active: ["The", "brilliant", "scientist", "discovered", "amazing", "results"]
Attention Matrix (6×6):
The bril sci disc amaz res
The [0.2 0.1 0.2 0.2 0.1 0.2]
brilliant[0.1 0.3 0.3 0.1 0.1 0.1]
scientist[0.1 0.2 0.4 0.2 0.0 0.1]
discovered[0.1 0.1 0.3 0.3 0.1 0.1]
amazing [0.2 0.2 0.1 0.1 0.2 0.2]
results [0.1 0.1 0.2 0.3 0.1 0.2]
KV Cache: 6 tokens × hidden_dim × 2After recursion 1, tokens with only 1 pass(“The”, “amazing”) exit and go to final layer
directly.
Recursion 2: Reduced Active Set
Active: ["brilliant", "scientist", "discovered", "results"]
Attention Matrix (4×4) - More focused!:
bril sci disc res
brilliant[0.4 0.3 0.2 0.1] ← More self-attention
scientist[0.2 0.5 0.2 0.1] ← Deep self-focus
discovered[0.1 0.3 0.4 0.2] ← Focuses on scientist
results [0.1 0.2 0.3 0.4] ← Focuses on discovered
KV Cache: Only 4 tokens × hidden_dim × 2 (33% less memory!)After recursion 2, tokens with 2 passes (“brilliant”, “discovered”, “results”) exit
Recusion 3: Deep Thinking
Active: ["scientist"] Attention Matrix (1×1): scientist[1.0] ← Pure self-attention, maximum depth processing KV Cache: Only 1 token × hidden_dim × 2 (83% less memory!)
Step 3: Memory Efficient Calculation
# Traditional Transformer (12 layers): traditional_memory = 6_tokens × 12_layers × hidden_dim × 2 # = 6 × 12 × 768 × 2 = 110,592 memory units # MoR (3 recursions): recursion_1_memory = 6_tokens × hidden_dim × 2 # All tokens recursion_2_memory = 4_tokens × hidden_dim × 2 # 4 tokens recursion_3_memory = 1_token × hidden_dim × 2 # 1 token mor_memory = recursion_1_memory + recursion_2_memory + recursion_3_memory # = (6 + 4 + 1) × 768 × 2 = 16,896 memory units memory_savings = (traditional_memory - mor_memory) / traditional_memory # = 84.7% memory reduction!
Numbers don’t lie…. Actual Results as per MOR research paper, https://arxiv.org/abs/2507.10524. I rest my case here with below results table….
Thanks very much for spending your valuable time to read my blog. Please do support this article with claps if you think you learned something from this blog.
Conclusion: Why MoR is the Future
Mixture-of-Recursions isn’t just an incremental improvement — it’s a paradigm shift that makes AI:
Smarter: Adaptive processing based on complexity
Faster: Up to 85% reduction in computation
Cheaper: 75% fewer parameters and memory
Scalable: Better handling of long sequences
Efficient: No wasted computation on simple tokens In a world where AI models are becoming increasingly large and expensive to run, MoR offers a path to intelligent efficiency. It’s not about making models bigger — it’s about making them smarter.
Just like how humans don’t think equally hard about every word they read, AI shouldn’t process every token with the same intensity. MoR finally brings this human-like adaptive intelligence to artificial neural networks.
The future of AI isn’t just about more parameters — it’s about using them more intelligently. And that future starts with Mixture-of-Recursions.